Tao Li’s Research Group from Nanjing University Demonstrated Control of Topological States in Type-II Weyl Heterostructures
High-dimensional heterostructures are rare, yet synthetic dimensions find the way.
Topological inversions are common, but optical confinement not always stay.
Interface modes appear and fade, while Weyl gapsdictate their rise and fall.
I possess waveguides that overturn dispersion, you discern through transparency the key.
Introduction:
Recently, a team led by Prof. Tao Li and Shining Zhu from Nanjing University, in collaboration with Prof. Luqi Yuan from Shanghai Jiao Tong University, has made significant progress in the control of topological photonic fields in waveguide arrays. They constructed artificial Weyl heterostructures using subwavelength grating waveguides and achieved control over the topological interface states of three-dimensional Type-II Weyl heterostructures in one-dimensional waveguide arrays, as well as the manipulation of light transmission and reflection at the interface. The manuscript entitled Bound-Extended Mode Transition in Type-II Synthetic Photonic Weyl Heterostructures is published on Phys. Rev. Lett. 132, 143801 (2024). Prof. Tao Li and Prof. Luqi Yuan are the corresponding authors of the paper. Dr. Wange Song is the first author. The work was meticulously guided by Prof. Shining Zhu.
Background:
Traditional topological theory suggests that topological boundary states arise due to band structure inversions at topologically distinct interfaces. When extending from lower to higher dimensions, the band structure becomes more complex, accompanied by richer physical phenomena. For instance, the existence of Weyl points has been observed in three-dimensional structures. Given the challenges of realizing and controlling Weyl points in nature, researchers have proposed using artificial microstructures and synthetic dimensions to construct Weyl points. This group had previously demonstrated a novel method for constructing new types of Weyl topological interface states through non-Hermitian control of synthetic dimensions (refer to Phys. Rev. Lett. 130, 043803 (2023)). Typically, band inversion is seen as a hallmark feature of topological states.
However, does band inversion always imply the presence of topological boundary states? In fact, for common topological structures, the inversion of topological bands and the presence of a bandgap are necessary conditions for the existence of topological boundary states. It is commonly believed that satisfying this condition will inevitably lead to the emergence of topological boundary (interface) states, which is considered a sufficient condition. Yet, this is not always the case. If the topological band structures on both sides of the interface change, this rule may no longer apply. For example, Type-II Weyl points have tilted bands, and their heterostructures may not satisfy the bandgap matching condition, suggesting that under certain conditions, the commonly occurring topological boundary states may disappear. This sets new rules for the existence of topological modes. Of course, how to construct Type-II Weyl heterostructures in the optical regime is also a significant challenge.
Results:
In this study, researchers used subwavelength grating (SWG) waveguides to construct Type-II Weyl points in the optical frequency range, revealing the topological phase transitions and interface effects within Type-II Weyl heterostructures. With the rich parameter space provided by SWG waveguides, researchers successfully constructed artificial Weyl heterostructures (Fig. 1a). More interestingly, by adjusting waveguide parameters such as duty cycle and width, they achieved abnormal waveguide "dispersion" (the mode constant decreases as the waveguide width increases, see Fig. 1b), which is key to realizing Type-II Weyl points (traditional waveguides only support Type-I Weyl points). Based on this, researchers demonstrated the phase transition process from Type-I to Type-II Weyl points by adjusting the parameters of SWG waveguides (Fig. 1c-e), and constructed Weyl heterostructures by connecting two independent Type-II Weyl media.
The research shows that, besides the topological phase transition, adjusting the relative rotational phase of the two Weyl media in parameter space can also control the emergence and disappearance of topological interface modes (Fig. 2a,b). This control mechanism originates from the tilted dispersion characteristics of Type-II Weyl structures, leading to complete (partial) matching or complete mismatch of bandgaps at different rotational phases (Fig. 2d). Therefore, although band inversion always exists, it does not necessarily result in topological states. In this case, the offset of the bandgap will determine the appearance and disappearance of topological states (Fig. 2e,f). In the Type-I case, as long as the topological orders are opposite, topological interface modes will always exist. Researchers further defined a band-shift index to precisely describe this unique topological state phase transition effect in Type-II Weyl systems (Fig. 2c).
The tilted dispersion of Type-II Weyl band structures also provides a new means to control light refraction and reflection at interfaces. For example, by choosing the rotational phase to cause complete mismatch of the bandgaps of the two Type-II Weyl media, a total reflection effect occurs at the interface, which has potential applications in light guiding functions based on Weyl materials. Additionally, in Type-II media, various phase choices can achieve partial reflection and full transmission phenomena, while Type-I Weyl media always maintain full transmission characteristics. All of these effects have been experimentally verified in on-chip silicon waveguides in the communication band (Fig. 3).
The Weyl heterostructures have already received widespread attention in condensed matter systems, with studies using their anisotropic band structures to regulate Andreev reflection properties and simulate gravity-related effects. This work opens up new avenues for studying high-dimensional topological phenomena, expands the existence and control flexibility of topological states, and will spark broad interest in fields such as condensed matter physics, integrated photonics, and quantum simulation.
This research is supported by the National Key R&D Program of China, the National Natural Science Foundation of China, Dengfeng Project B of Nanjing University.
Article Link:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.143801
Quick view of the images:
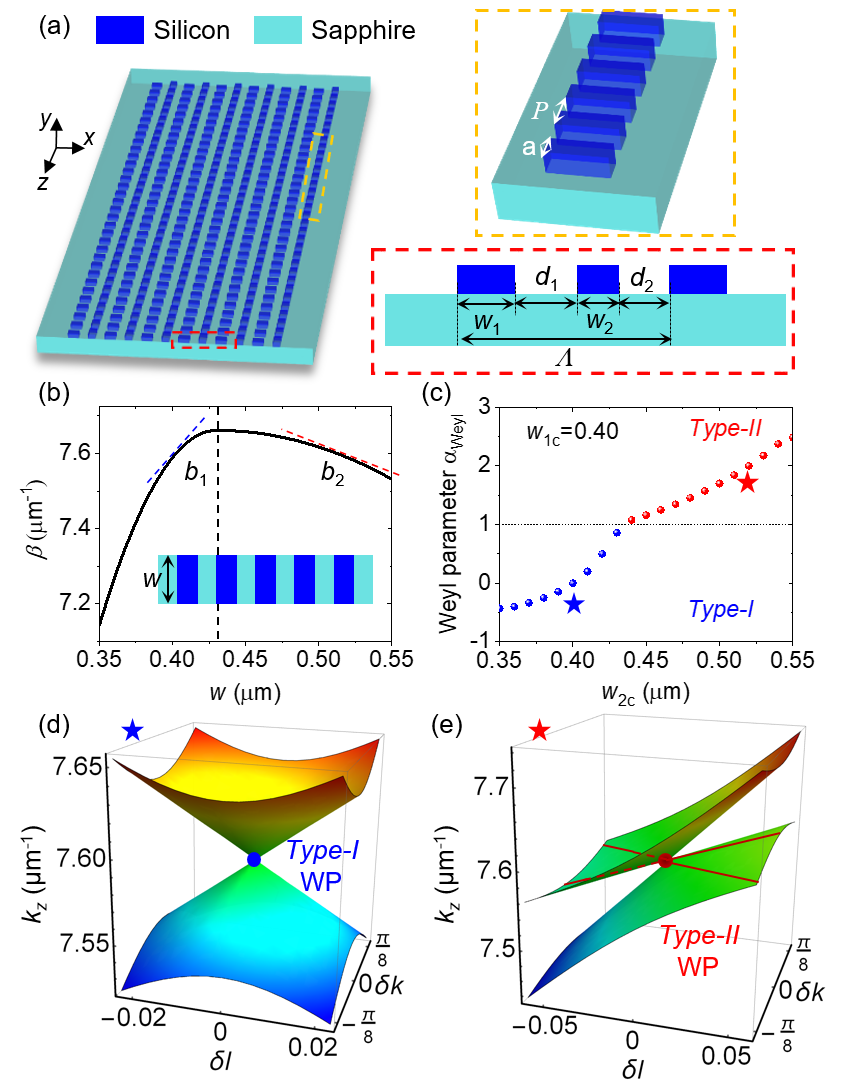
Fig. 1: Construction of Type-II Weyl points using SWG waveguides in parameter space.
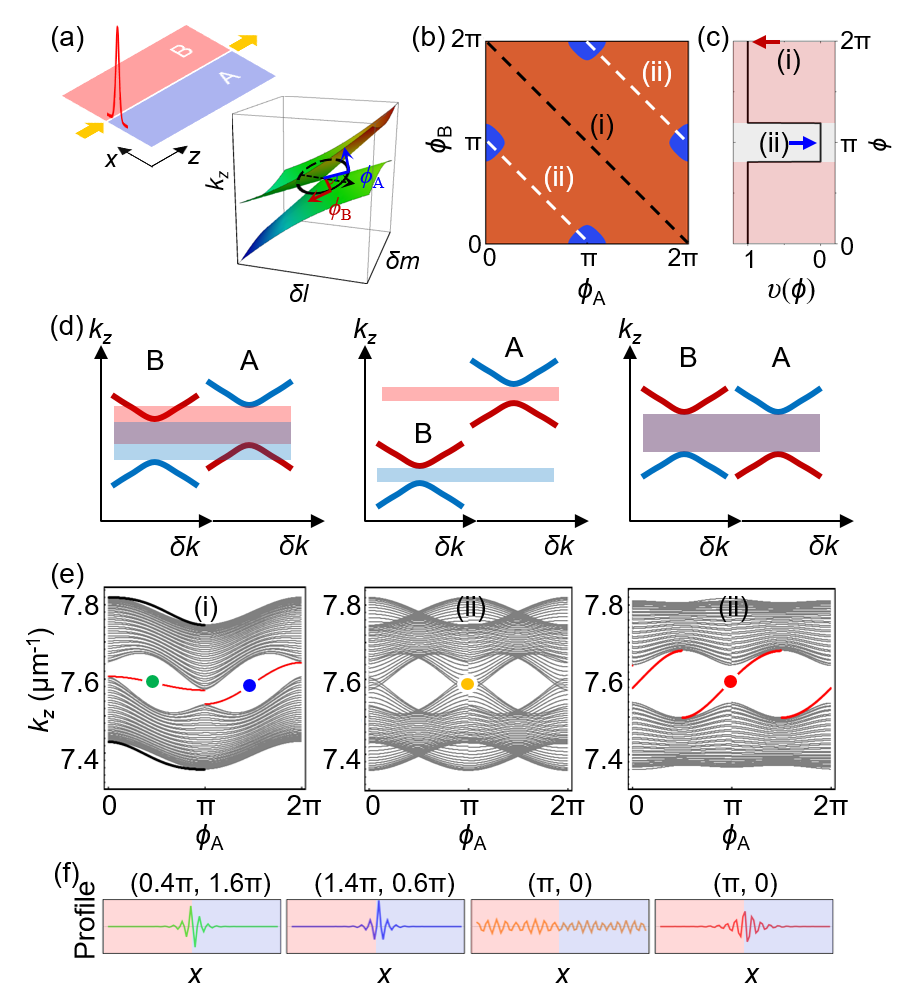
Fig. 2: Demonstration of bound state-bulk state transitions in Type-II Weyl heterostructures.
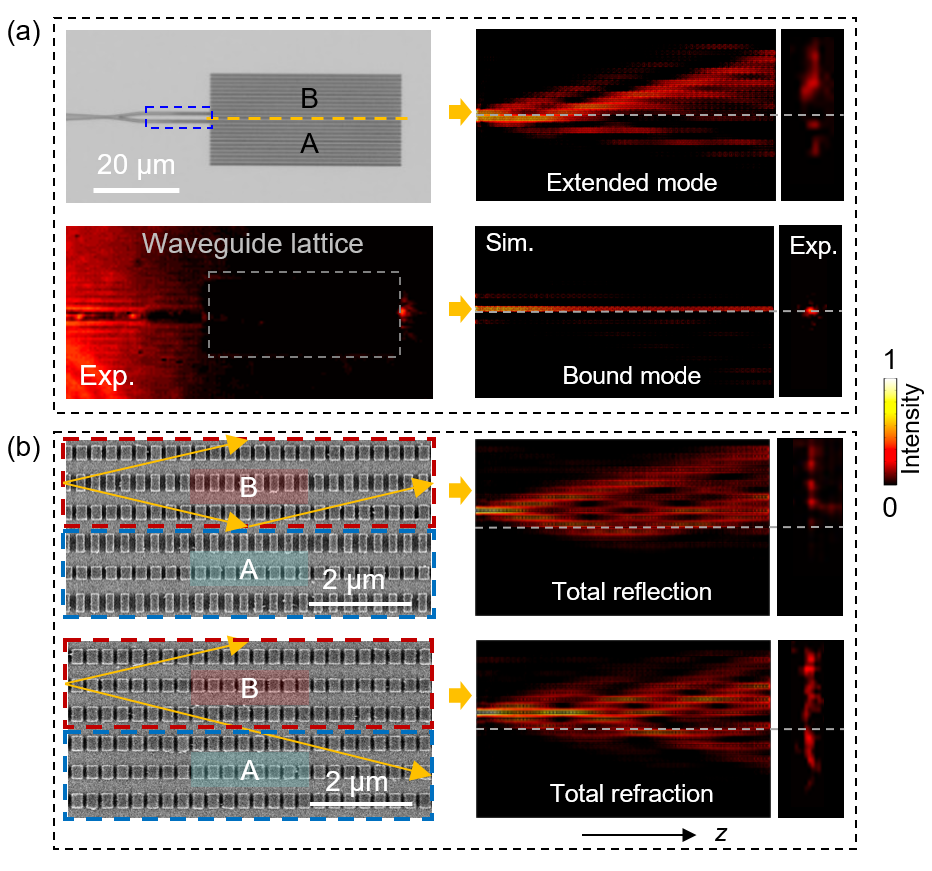
Fig. 3: Experimental results.
(Submitted by Tao Li’s Group)

