On 14th October 2019, the national prestigious journal of Physics Physical Review Letters published the latest work titled as Breakup and recovery of topological zero modes in finite non-Hermitian optical lattices of Prof. Tao Li amd Shining Zhu’s research groups of College of Engineering and Applied Science, reporting the important progress in non-Hermitian topological photonics. They realized the recovery of edge zero modes of the deviated topological boundary by introducing the non-Hermitian loss modulation into the silicon waveguides, and verified its robust propagation characteristic. The paper was strongly recommended on the homepage of PRL as Editors’ Suggestion. Grade 16 bachelor-straight-to-doctorate student Wange Song is the first author. Prof. Tao Li is the corresponding author. Prof. Shumin Xiao and Prof. Qinghai Song of Harbin Institute of Technology( Shenzhen) joined in the research of this subject as well. Doctor student Wenzhao Sun of Harbin Institute of Technology( Shenzhen), as well as grade 16 bachelor-straight-to-doctorate student Chen Chen of College of Engineering and Applied Science also contribute a lot to the paper.

Non-Hermitian and topology are two leading concepts in quantum mechanics and condensed matter physics. In recent years, PT(parity time)-symmetric systems with non-Hermitian Hamiltonian have attracted more and more attention. Among them, the modulated optical system with gain and loss has become an important platform for studying PT symmetry. The introduction of PT symmetry also provides abundant approaches for the regulation of novel photon states. On the other hand, the edge states in topological artificial microstructures exhibit topological protection, which enables photonic systemswith a robust behavior in propagation and brings hope to the future robust photonic chips. However, as the size of the system decreases, these edge states tend to couple with each other, which willweaken topological protection to some extent. For example, in a one-dimensional(1D) topological systems, thoseedge states at the zero-energy point pinned in the middle of the band gap, are usually called zero modes. It exhibitsgreat spatial localization and topological protection. Nevertheless, in actual finite systems, due to the existence of coupling effect, zero modes may deviate from the exact-zero energy. Since the topological protection of zero modes dependson its zero energyto a large extent, the deviationfrom zero energy will inevitably weaken topological protection. Therefore, to clarify the coupling characteristic between topological edge states in a finite topological system and to strengthen its topological protection are urgent problems in this field.
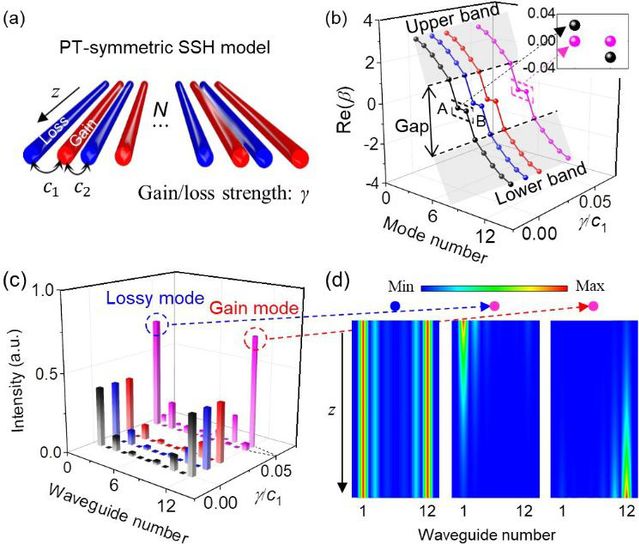
Figure 1 Recovery of zero modes by non-Hermitian modulation in finite systems
Non-Hermitian PT-symmetric Su-Schriffer-Heeger ( SSH ) model;
Band and (c) Edge states filed distribution with respect to γ/ C1;
Evolution of near- and exact-zero mode
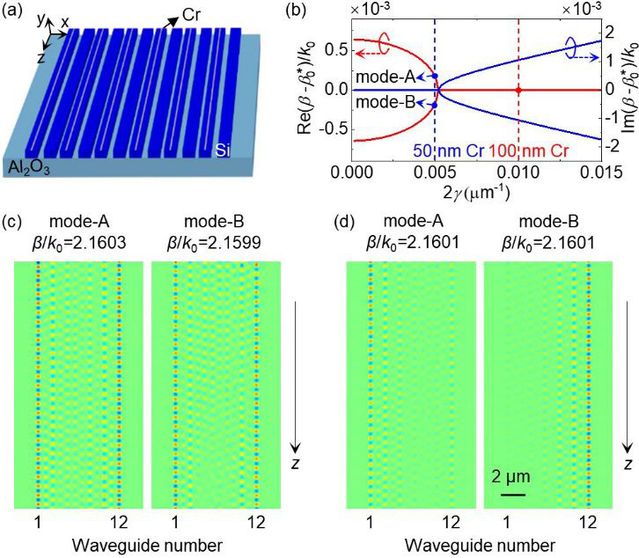
Figure 2 Theoretical model and simulation results
Non-Hermitian optical lattice consisting of a silicon waveguide array coated by chrome (Cr) layer;(b) Theoretical mode spectrum of the mode constant as functions of the loss strength;(c,d) The evolution of exact-zero and near-zero modes through non-Hermitian modulation in silicon waveguides
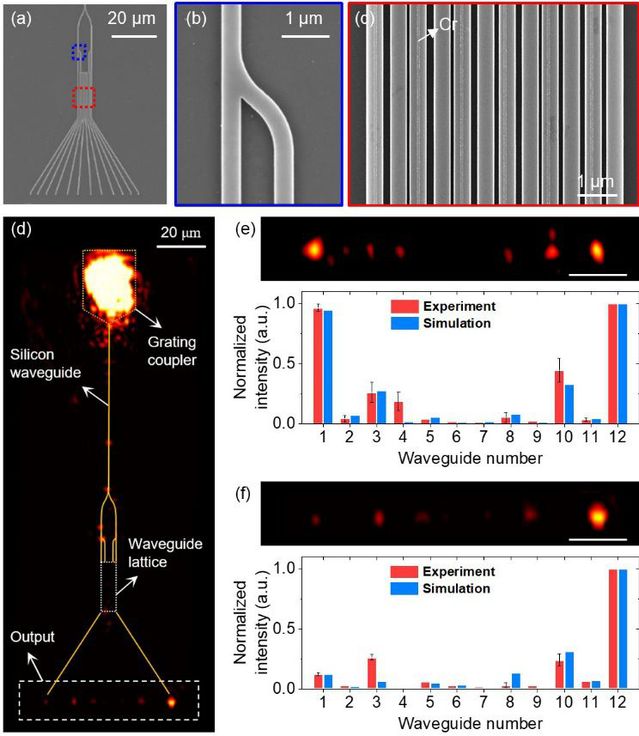
Figure 3 Experimental results
(a-c) SEM images of the sample;(d) CCD recorded optical
propagation of the system; Experimentally detected output intensities of (e) near-zero and (f) exact-zero modes.
This workconfirms the zeromodesdeviation caused by the coupling of finite systems in the 1D topological waveguide lattice, and proposes a solution ,that is, recovering to exact-zeromodes by introducing non-Hermitian degeneracy with PT symmetry. The work first constructed the optical waveguides through the Su-Schriffer-Heeger (SSH) model, theoretically analyzed the effects of zero-mode splitting due to edge states coupling in finiteHermitian systems, and then introduces non-Hermitianmodulation (gain and loss) into SSH systemsto realize recovery from near-zero mode to exact-zero mode. The paper elaborates on mode constants, mode distribution and the evolution of edge states during the transition process from near-zero modes to exact-zero modes in the system, which establishes a solid theoretical framework. Then the paper carries out detailed simulation and experiments based on silicon waveguides [Fig.2 and Figu. 3], and makes a clear comparison between the Hermitian and non-hermitian situations. It tells that the experimental results are very consistent with the theoretical predictions. Both theory and experiment suggest that the exact-zero modes obtained by non-Hermitian modulation exhibits better propagation robustness than the near-zero modesin the Hermitian system when introducing structural deviation and disorder. This workcould deepen people's understanding of the coupling characteristic of topological edge states and has universal scientific significance. This work shows that the manipulation of non-Hermitian parameters can realize flexible control of photonic topological properties and provides a theoretical basis for further in-depth study of the correlation between topology and PT. Considering that many practical topological systems have limited size. Therefore the scheme proposed by this paper has strong practical importance and potential applications.
The research is supported by the National Key Research and Development Program of China, the National Natural Science Foundation of China, and the Mountain-Climbing Talents Program of Nanjing University.
(Source: "Imeta-center" WeChat Official Account)

