材料科学与工程系、固体微结构物理国家重点实验室、南京微结构科学与技术协同创新中心周健副教授、陈延峰教授研究组在量子化拓扑霍尔效应方面取得重要进展:该结果以《Predicted Quantum Topological Hall Effect and Noncoplanar Antiferromagnetism in K0.5RhO2》为题,于2016年6月20日发表在《Physical Review Letters》[116, 256601 (2016)]。
霍尔效应(Hall effect)是指在一个通有电流的导体中,如果施加垂直磁场,则在垂直于磁场和电流的方向上产生一个横向电压的现象。这一现象由E. H. Hall于1879年发现,次年他进一步发现:在铁磁导体中的霍尔效应远大于非磁材料,甚至在不加外磁场时也会有霍尔效应,被称为反常霍尔效应(anomalous Hall effect)。对于霍尔效应,可以用简单的洛伦磁力来解释,而本征的反常霍尔效应则需要利用电子的自旋轨道耦合和Berry曲率才能够得到解释。
在霍尔效应发现100年后,德国物理学家von Klitzing于1980年发现了量子霍尔效应,即整数量子霍尔效应。美籍华裔物理学家崔琦则于1982年发现了分数量子霍尔效应。对应于反常霍尔效应的量子化更为扑朔迷离,直到2013年,我国清华大学和中科院物理所的研究团队才在铁磁掺杂的拓扑绝缘体(Cr掺杂(Bi,Sb)2Te3)中实现了量子化反常霍尔效应(quantum anomalous Hall effect, QAHE),从而成为继量子霍尔效应、量子自旋霍尔效应之后的“量子霍尔效应家族的最后一位成员”。
但事实上,反常霍尔效应可以更“反常”。2001年,东京大学Nagaosa教授等提出:如果一个巡游电子经过一个非共面磁结构,就会获得一个Berry相位 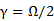 ,其中
,其中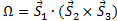 代表三个自旋矢量张成的立体角,也就是scalar spin chirality,如图1所示。这个Berry相位等效于一个外磁场,从而可以产生巨大的反常霍尔效应。人们把这种由非共面磁性所造成的反常霍尔效应称之为非常规的反常霍尔效应(unconventional anomalous Hall effect)或者拓扑霍尔效应(topological anomalous Hall effect, THE)。目前人们已经在多个体系中证实了THE的存在。比如最近在室温下观察到Mn3Sn中具有的巨大的反常霍尔效应就是来自于这种非共面磁性。在Skyrmions体系中也观察到了THE。
代表三个自旋矢量张成的立体角,也就是scalar spin chirality,如图1所示。这个Berry相位等效于一个外磁场,从而可以产生巨大的反常霍尔效应。人们把这种由非共面磁性所造成的反常霍尔效应称之为非常规的反常霍尔效应(unconventional anomalous Hall effect)或者拓扑霍尔效应(topological anomalous Hall effect, THE)。目前人们已经在多个体系中证实了THE的存在。比如最近在室温下观察到Mn3Sn中具有的巨大的反常霍尔效应就是来自于这种非共面磁性。在Skyrmions体系中也观察到了THE。
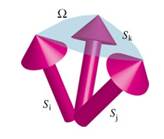
图1. 三个非共面的磁矩张成一个立体角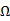 。
。
那么这种“反常”的反常霍尔效应是否可以实现量子化呢,即是否存在量子化拓扑霍尔效应(quantum topological Hall effect, QTHE)呢?目前关于这方面的研究非常少。而我们的工作第一次通过第一性原理计算预测层状Rh氧化物材料K0.5RhO2可能会具有QTHE。
KxRhO2是一个由RhO2层和K层交替排列形成的层状材料(图2(a)),其中RhO2层形成二维的三角晶格。当x=0.5时,我们通过计算并比较了大量不同磁结构的能量,发现该材料具有一个特别的磁基态:全出/全进的非共面反铁磁(图2(a)和(b)),该磁结构元胞为晶体学元胞的4倍(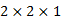 )。从能带上看,该材料具有一个0.22 eV左右的能隙,而且在能隙中,具有量子化的反常霍尔电导
)。从能带上看,该材料具有一个0.22 eV左右的能隙,而且在能隙中,具有量子化的反常霍尔电导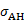 ,(图2(d))。我们计算了该体系的陈数,发现一个元胞中的陈数是2,这是因为一个元胞里有两层RhO2,每一层的陈数为1,所以总的陈数为2。理论上预言,具有非零陈数的体系可表现为内部是很好的体态绝缘性质,而在边界上存在手性拓扑导电态,可无耗散地传输电流从而极大地降低器件的能耗,因此在材料科学和电子学中具有巨大的应用潜力。
,(图2(d))。我们计算了该体系的陈数,发现一个元胞中的陈数是2,这是因为一个元胞里有两层RhO2,每一层的陈数为1,所以总的陈数为2。理论上预言,具有非零陈数的体系可表现为内部是很好的体态绝缘性质,而在边界上存在手性拓扑导电态,可无耗散地传输电流从而极大地降低器件的能耗,因此在材料科学和电子学中具有巨大的应用潜力。
在上述的计算中,我们并没有包含自旋轨道耦合,非共面的磁结构来自于三角晶格的自旋阻错。如果进一步考虑到自旋轨道耦合的作用,则结果类似(如图2(e))。通过简单的海森堡模型估算出该体系磁结构的奈耳温度在20 K左右,远高于目前实验上的Cr掺杂(Bi,Sb)2Te3体系的温度。
因此,我们通过第一性原理预测:K0.5RhO2中可能存在一种新的QAHE—即QTHE。该效应的特别之处在于:它不需要自旋轨道耦合,也不需要系统具有净磁矩或者铁磁性,完全可以在净磁矩为零的反铁磁材料中实现QAHE。该工作为实验上寻找其它的QAHE体系提供了新的思路。
我们周健副教授和绍兴文理学院物理系梁奇锋副教授为共同第一作者,我们陈延峰教授和台湾大学物理系郭光宇教授为共同通讯作者,北京物理所翁红明研究员、我们姚淑华副教授、物理学院陈延彬副教授和董锦明教授参与了本工作。本工作得到了项目得到了国家重点基础研究发展计划(973计划)和国家自然科学基金委项目等基金的支持。
论文连接:http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.256601
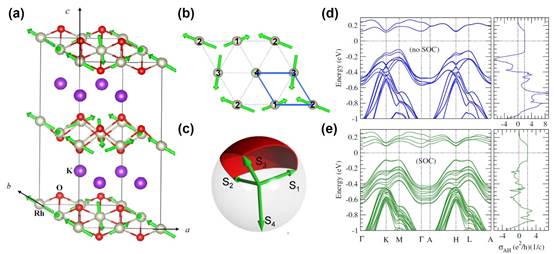
图2. (a) K0.5RhO2的全出/全进的磁结构元胞,绿色箭头代表Rh离子磁矩的方向;(b) 一层RhO2层形成的三角晶格及其磁矩;(c) 一层RhO2层中四个Rh离子上的磁矩张成一个Bloch球面,其立体角为4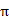 ,因此对应的Berry相位为2
,因此对应的Berry相位为2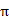 ,陈数为1;(d) 不考虑自旋轨道耦合时,全出/全进磁结构的能带图(左)和对应的反常霍尔电导随费米能的变化;(e)同图(d)类似,但是考虑了自旋轨道耦合效应。
,陈数为1;(d) 不考虑自旋轨道耦合时,全出/全进磁结构的能带图(左)和对应的反常霍尔电导随费米能的变化;(e)同图(d)类似,但是考虑了自旋轨道耦合效应。


